IB HL PHYSICS T2 THERMO NOTES

NOTES AND QUESTIONS FOR CRAMMING THERMAL PHYSICS

Random Mechanics Problems

A rigid tube is placed in the vertical plane. It has the shape of an arbitrary curve, but has start and end points of the same height. A chain with uniform mass distribution lies in the tube. Show that the chain lies stationary in the tube, no matter its shape.

Solution can be found here.

A stick of mass density per unit length  rests on a circle of radius R. The stick makes an angle  with the horizontal and is tangent to the circle at its upper end. Friction exists at all points of contact, and assume that it is large enough to keep the system at rest. Find the friction force between the ground and the circle.

Solution can be found here.

A large number of sticks (with mass density per unit length p and circles (with radius R) lean on each other. Each stick makes an angle with the horizontal and is tangent to the next circle at its upper end. The sticks are hinged to the ground, and every other surface is frictionless. In the limit of a very large number of sticks and circles, what is the normal force between a stick and the circle it rests on, very far to the right? Assume that the last circle leans against a wall, to keep it from moving.

Solution can be found here.

Derivation of Ideal Gas Equation

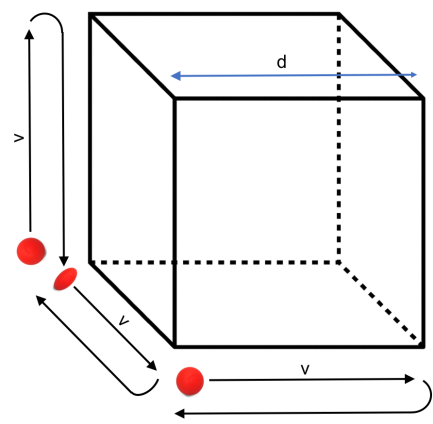
Let this cube resemble an ideal gas, and one red molecule represents one of the monoatomic gas particles in the gas moving in constant random motion.

To simplify the problem, let’s consider one molecule of a monoatomic gas in a 1D plane,

Let d be the length of one side of the cube.

As such,

where v = the velocity of a particle moving in constant random motion,

and t = the time taken for a particle to travel along one side of the cube and back to its original position.

Let F be the force by the walls of the box on the particle that causes the particle to change direction.  By Newton’s third law, this is equal to the force of the particle on the wall.

By applying Newton’s second law of motion,

The pressure caused by the gas moving in a straight line and striking the wall perpendicularly is:

However, this resulting equation can only be applied in a 1D plane.

To apply this equation to 3D,

Since the velocity squared of the particle has an equal chance of being directed in any of the three dimensions, and it has an equal chance of hitting any of the three walls and causing pressure in any of the three dimensions, we multiply the equation by 1/3.

The pressure caused by N molecules of monoatomic gas can be given by multiplying the equation by N:

Based on statistics (Maxwell-Boltzmann distribution curve),

Taken from: http://revisionworld.com/a2-level-level-revision/chemistry/energy-changes/maxwell-boltzmann-distribution

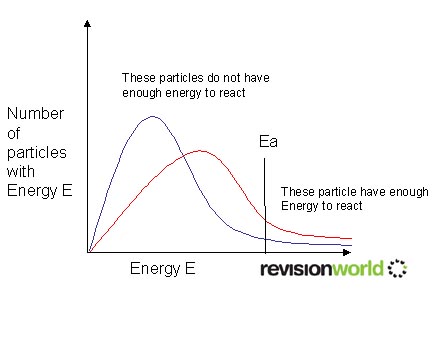
Assuming that all the particles act independently of each other, as no intermolecular forces are present, we can multiply the average kinetic energy, which is proportional to T, by N to find total kinetic energy.

Hence, 

Finally, by putting the two equations together, we obtain the ideal gas equation:

Questions for Mechanics (1)

CONSEQUENCES OF NEWTON’S LAWS 

In reference to inertial reference frame X : Point mass A, 3kg, travels right at 5m/s. Point mass B,4kg, travels left at 20 m/s.

1. What is the total momentum in the system in reference to frame X?
2. A frame Y is defined as moving leftwards at velocity V relative to frame X. In frame Y, the sum momentum of masses A and B is zero. What is the value of V, and what is the momentum of mass B in reference to frame Y?

A man of mass 100kg stands at the leftmost tip of a stationary boat with mass 700kg. The boat is 16m in length. If the man walks to a point 2m from the right end of the boat, what is the total displacement of the boat?

FORCES AND FREE-BODY DIAGRAMS

A ladder is left stationary on a rough floor, leaning on a rough wall. It has a mass M.

1. What is the coupled action-reaction pair force corresponding to the weight of the ladder?
2. Draw a free body diagram of the ladder, displaying all forces at both points of contact of the ladder with the floor and wall. [hint : include the weight of the ladder, and all frictional and normal forces]
3. The coefficient of friction of the ladder against the floor and wall are μf and μw, respectively. Let the normal forces at the floor and wall be Nf and Nw, respectively. Assuming that the ladder is just at the equilibrium point before slipping at both contact points, form two equations relating :
   1. all the horizontal forces involved.
   2. all the vertical forces involved.
4. If μf = 0.6 and μw = 0.4, What are the values of Nw and Fw?

A ladder is left stationary on a rough floor, leaning against a perfectly smooth wall. It has an even mass distribution along its length L, and a mass of M. It forms an angle θ with the horizontal. Let its point of contact with the ground be G.

1. Draw a free body diagram of the ladder, displaying all forces at both points of contact of the ladder with the floor and wall.
2. Express the turning moment of the ladder about G, due to Nw.
3. Express the turning moment of the ladder about G, due to the weight of the ladder.
4. Noting that the system is in rotationary equilibrium, express Nw in terms of θ and its weight.
5. Let the mass of the ladder be 5kg. If θ = 60 °, what is the value of Nw?

 

 

Questions for Capacitance

 

A capacitor has initial capacitance C. A dielectric of dielectric constant 4 is pushed between the plates so that it covers a quarter of the capacitor’s area. What is the new capacitance in terms of C?

A capacitor is charged to 12V and disconnected from the battery. Its plates are then pushed together such that their new separation is half as big as initially. What is the new potential difference across the capacitor?

A capacitor is charged to 3V, 12 μF using a 3V power supply. It is then disconnected and re-connected to a 6V power supply, where it continues charging. Assuming that the capacitor does not break down, what is the work done as it charges from 3V to 6V?

A capacitor C₁ of capacitance C is connected to a 12V source and allowed to charge fully. It is then disconnected from the source and connected with an uncharged identical capacitor C₂. How much charge, in terms of C, is now on C₂? What is the new potential difference across C₁?

A capacitor C₁ of capacitance C is connected to a 6V source and allowed to charge fully. It is then disconnected from the source and connected with an uncharged identical capacitance C₂ of capacitance C/2. How much charge, in terms of C, is now on C₂?

A capacitor C₁ of capacitance C is connected to a 10V source and allowed to charge fully. A capacitor C₂ of capacitance 3C/4 is connected to a 12V source and allowed to charge fully.

1. The two are then connected with their positively-charged plates touching. How much charge are on capacitors C₁ and C₂ each?
2. Should the two have been connected with oppositely-charge plates touching, how much charge would have been on capacitors C₁ and C₂ each?

Three capacitors C₁, C₂, and C₃ with respective capacitances of 6 μF, 12 μF and 10 μF are connected in series across a 14V supply.

1. How much charge accumulates on C₂?
2. What is the potential difference across C₃?

The three capacitors are now disconnected. C₁’s positive plate is connected to touch C₂’s negative plate. C₃’s positive plate touches C₂’s positive plate, and C₃’s negative plate touches C₁’s negative plate.

1. What is the total capacitance of C₁ and C₂?
2. How much charge accumulates on C₃?
3. What is the voltage across C₁ and C₂ combined?
4. What is the voltage across C₁ alone?
5. How much energy is stored in C₁?

A uncharged capacitor of capacitance 6 μF is connected to a 6V battery and a 2Ω resistor. In the midst of charging, it holds 2.4·10^-5 C of charge. How much time has passed since it began charging?

A capacitor of capacitance C and initial charge Q_i is connected in series with a 6V power supply and a 2Ω resistor.

1. What is the potential difference across the capacitor?
2. Assume that the potential difference across the capacitor is smaller than 6V. Is the capacitor charging or discharging?

An uncharged capacitor of capacitance 6 μF is connected in series with a 10V power supply and a 3Ω resistor. What is the maximum amount of charge in can attain in this circuit? What is the time taken for it to charge up to half this amount?

Questions for Thermodynamics (4)

IDEAL GAS LAW, HEAT TRANSFER

1. How would the P-T graph of a real gas differ from that of an ideal gas? Draw the two graphs on P-T axes.
2. The root mean square speed of a sample of Helium atoms is 1.36 x 10³ m/s. The molar mass of helium is 4g/mol.
   1. What is the temperature of the sample of Helium gas?
   2. Another sample of Oxygen gas is at the same temperature. Treating Oxygen gas as monoatomic, with molar mass 16g/mol, what is the rms speed of the molecules?
   3. Would there be a difference in the rms speed of the Oxygen molecules if they were assumed to be diatomic? And why?

FIRST LAW OF THERMODYNAMICS

1. One mole of an ideal gas is initially at characteristics P1, V1 and T1. Keeping its temperature constant, it is allowed to expand to three times its initial volume. Express the work done by the gas on the environment in terms of R,T1, P1 and V1.
2. An ideal gas is kept in contact with a thermal reservoir and allowed to do 60J of work on its surroundings. How much heat flows from the thermal reservoir into the gas?
3. One mole of a gas is insulated from the environment, and compressed such that 50J of work is done on it. Assume that its molar heat capacity stays constant at 20J/mol. What is its temperature change?
4. On P-V axes for an ideal gas :
   1. Draw three P-V graphs for three different temperatures, and label them T1 T2 and T3 in order of ascending temperature.
   2. Define a point on the T2 isotherm as the initial characteristics of the gas. Draw the following gas manipulations : Placed in contact with a thermal reservoir, the gas is allowed to expand to twice its volume.
   3. The gas is then compressed to half its volume extremely quickly, such that no heat is exchanged with its surroundings.
   4. The size of the box is now fixed, the gas is placed in contact with a thermal reservoir half its temperature, and allowed to reach equilibrium.
   5. With it pressure kept constant, it is now allowed to expand to 1.5 times its volume.
   6. Shade the area representing the work done by the gas on its surroundings in steps 2 and 5.
5. Would you predict molar heat capacity at constant pressure or volume to be greater? And why?

HEAT ENGINES, CARNOT CYCLE

1. A heat engine does 50J of work and expels 100J of energy into its lower temperature reservoir. What is its efficiency? If its lower temperature reservoir is at 100K, what temperature is its higher temperature reservoir at?
2. A heat engine operating at 80% efficiency takes in 100J of energy. How much energy is used to do useful work? What is the ratio between the temperatures of its low- and high- temperature reservoirs?

SECOND LAW OF THERMODYNAMICS, ENTROPY

1. When water freezes, its molecules get fixed in a more regular pattern. Why does this not contradict the second law of thermodynamics?
2. A fridge is turned on and left open in a room for  ten hours. After that, it is turned off and left there for another ten hours. How does the entropy in the room change in the first ten hours and after the second ten hours?

Questions for Thermodynamics (3)

SCHOOL-LEVEL QUESTIONS

1. Liquid X has a specific heat capacity Cx. It is mixed with an equal mass of liquid Y with specific heat capacity Cy. The temperature of X is initially greater than that of Y. What is the ratio of the temperature rise of  X over that of Y? Express this in terms of the two heat capacities.
2. What is the average kinetic energy of water molecules at 120C?
3. A bullet is fired into an iron plate, where it deforms and finally stops. As a result, the temperature of the bullet increases by an amount dT1. A bullet having twice the mass and half the speed causes the temperature change dT2. What is the ratio dT2/dT1 ?
4. A block of metal at 90C is placed in a beaker of water of the same mass at 0C. The final temperature of the water and block are 9C. Assuming that this system is isolated from its surroundings, what is the ratio of the specific heat of the water to the specific heat of the metal?
5. The kinetic energy of gas A with molar mass 3, at temperature T, is K. The kinetic energy of gas B with molar mass 5, at temperature T, is k. What is the ratio K/k ?
6. As altitude increases, does the latent heat of vaporisation of a gas increase or decrease?

HEAT ENGINES AND ENTROPY

1. During each cycle, a heat engine absorbs 400J from a high-temperature reservoir and discards 350J into its low-temperature reservoir. What is its efficiency?
2. An engine of efficiency 25% discards 75J of heat into its low-temperature reservoir in every cycle. How much heat does it absorb per cycle?
3. A carnot cycle operates between the temperatures of 500K and 300K. If it absorbs 10J of heat at the start of every cycle, how much heat does it discard at the end?
4. A refrigerator is left with its door open in an insulated room. At the end of 24hrs, how has the temperature and entropy of the room in total changed?

A Random Mechanics Question

(adapted from STEP I, 2009 Q9)

A child plays with a toy cannon on the floor of a long railway carriage, moving north with the acceleration a. The cannon is pointed south at an angle θ to the horizontal. It fires a shell at speed v.

1. Give an expression for the range of the shell in the carriage. [in terms of v, θ, g and a]
2. Find the value of tan(2θ) that maximises the range of the shell in the carriage. [hint : its just differentiation]

Questions for Thermodynamics (2)

HEAT CAPACITIES

1. With reference to the two different gas manipulations, isochloric and isobaric, explain why two different values of specific molar heat capacity are required to show the relation between the heat flow into a gas and the temperature change it experiences.
   • [hint : in an isochloric expansion, the volume of the gas is fixed and it does no work on its surroundings while being heated. in an isobaric expansion, however, it expands at a constant pressure.]
2. Let CV be the specific molar heat capacity for an isochloric expansion, and CP be the specific molar heat capacity for an isochloric expansion. Show that CP = CV + R where R is the gas constant.
   • [hint : the work done in an isochloric expansion can be found WD = P dV.]
   • [hint : from the ideal gas equation where P is constant, P dV = nR dT.]
3. Why does the molar specific heat capacity of a monoatomic gas differ from that of a diatomic gas?
   • [hint :  how do their kinetic energies differ?]

IDEAL GAS MANIPULATIONS 

1.  On P-V axes for an ideal gas with a constant number of molecules :
   1. Draw an isotherm and define a point (V1, P1) on it.
   2. Draw a line representing the P-V states of the gas as it expands isothermally to V2 > V1.
   3. Shade the area on the graph corresponding to the work done by the gas as it expands isothermally from V1 to V2. Denote this area A.
   4. Give an expression for the amount of heat flow into the gas as it undergoes the previous transition. [hint : change in internal energy of the gas is zero. the WD integral can be evaluated using logarithmic forms.]
   5. Draw a line representing the P-V states of the gas as it expands adiabatically from (V1, P1) to (V2, P3).
   6. Shade the area on the graph corresponding to the work done by the gas as it expands adiabatically from V1 to V2. Denote this area B.
   7. Explain why A > B.
2. A fixed amount of ideal gas is placed in a one chamber of a bipartite container and thermally isolated from its surroundings. A shutter separates the two, and one of the chambers is evacuated (all molecules are removed from it).  The shutter is then opened and the gas allowed to pass into the other chamber. State :
   1. The work done by the gas on its surroundings.
   2. The heat flow to or from the gas.
   3. The change in internal energy of the gas.

Questions for Thermodynamics (1)

IDEAL GAS LAW

1. Draw three P-V graphs for a an ideal gas (with number of molecules constant) at three different temperatures.
2. Draw three P-T graphs for a an ideal gas (with number of molecules constant) at three different volumes.
3. Draw three P-T graphs for a an ideal gas (with number of molecules constant) at three different volumes.
4. On the three-dimensional axes of P, V, and T, draw a surface reflecting all the points that an ideal gas (with number of molecules constant) can exist at.
   • [hint : this will be easier to imagine with P axis positive upwards, V axis positive sideways, and T axis positive backwards]
   • [hint : the projection of the 3D surface onto the P-V plane for three different T values is the graph produced in question 1. same goes with corresponding variables in questions 2 and 3.]

FIRST LAW OF THERMODYNAMICS

1. 5g of a gas with heat capacity 0.9J/K is kept at a constant volume, and its temperature falls from 293K to 273K. Assuming that it is ideal, what is its change in internal energy?
2. 02.g of a gas with heat capacity 1.2kJ/K and molar mass 20g/mol is placed in a container of volume 0.5L and initial temperature 300K. It is allowed to expand to a volume of 1L with its temperature held constant. Afterwards, it is cooled to 250K with its volume held constant.
   1. How does the speed of the molecules in the gas change as it expands?
   2. How does the speed of the molecules in the gas change as it cools?
   3. What is the net change in the internal energy of the gas after the entire process?